Problem 7.18#
To find the weights for the \(n+1\) GLL points we need to evaluate
for which \(\ell^n_\alpha\) is a Lagrange polynomial. There is no good python function for computing Lagrange polynomials, so we will need to make our own. To compute the lagrange polynomials of degree \(n\), we require the control points (GLL points) that define it. This means we need a function to compute the relevant GLL points also. In fact, this is what Problem 7.17 asks you to do. To avoid importing functions, we will copy the function that generates gll points below. Please refer to Problem 7.17 for details
Show code cell source
import scipy.special as ss
import numpy as np
from copy import copy
import matplotlib.pyplot as plt
def gll(N, Nsegs=100):
# This function is the solution to 7.17.
# It is not the most efficient way to compute GLL points,
# but it works!
nroots = n + 1 # Number of roots
roots = np.zeros(nroots) # Array to hold all the roots
leg_n = ss.legendre(n) # P_n
leg_n_1 = ss.legendre(n-1) # P_{n-1}
def compute_functional(xi, n, lnm1, ln):
return n * (lnm1(xi) - xi * ln(xi))
# End points
roots[0] = -1
roots[-1] = 1
nrts_found = 2
if nroots > 3:
xi_end = 0.99999
if n%2==0:
xi_start = 0.00001
nrts_found += 1
else:
xi_start = 0.0
segments = np.linspace(xi_start, xi_end, Nsegs)
fseg = compute_functional(segments, n, leg_n_1, leg_n)
# Index in the 'roots' array to store the root
idx = int(nroots / 2) + nroots%2
# Loop through each segment and test if root lies within
for iseg in range(Nsegs-1):
if fseg[iseg] == 0:
# Root found exactly here
error = 0
nrts_found += 1
elif fseg[iseg+1] == 0:
# Root found exactly here
error = 0
nrts_found += 1
elif fseg[iseg] * fseg[iseg+1] < 0:
# There is a change in sign between the two values:
# Start with the current edge xi positions of the 'segment'
a = segments[iseg]
b = segments[iseg+1]
error = 999
while np.abs(error) > 1e-9:
grad = compute_functional(b, n, leg_n_1, leg_n) \
- compute_functional(a, n, leg_n_1, leg_n)
this_root = a + (b-a)/2
error = compute_functional(this_root, n, leg_n_1, leg_n)
if error !=0:
if grad*error > 0:
b = copy(this_root)
else:
a = copy(this_root)
roots[idx] = this_root
idx += 1
nrts_found+=2
for irt in range(1, int(n/2) + n%2):
i1 = int(nroots/2) -irt
i2 = int(nroots/2) +irt - n%2
roots[i1] = -roots[i2]
return roots
Next, lets write a function to compute the Lagrange polynomials:
def lagrange(N, a, x, GLL):
# Computes a'th Lagrange polynomial of degree N at points x
# using control points specified in GLL array
poly = 1
for j in range(0, N+1):
if j != a:
poly = poly * ((x - GLL[j]) / (GLL[a] - GLL[j]))
return poly
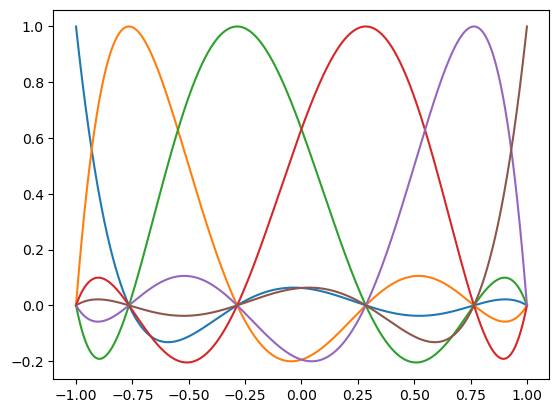
Now this is all set up, its straightforward to compute the weights. Let us define a value for \(n\), and compute the lagrange polynomials over the interval \([-1, 1]\). From this, we can integrate to compute the weights:
# N value defining the lagrange polynomials
n = 5
# Compute the n+1 GLL points
gllpts = gll(n)
# Define the domain interval [-1, +1] on 1000 points:
x = np.linspace(-1, 1, 1000)
# We will plot the Lagrange polynomials to check they are correct
fig, ax = plt.subplots()
print(f'Weights for degree {n}: ')
# Loop over the n+1 polynomials to compute the weights
for alpha in range(n+1):
# Integrand is simply the alpha'th lagrange polynomial of degree n
integrand = lagrange(n, alpha, x, gllpts)
# Plot lagrange polynomials as sanity check
ax.plot(x, integrand)
# Trapezoid rule to integrate
weight = np.trapz(y=integrand, x=x)
print(alpha, weight)
Weights for degree 5:
0 0.06666900466679278
1 0.37847201994856156
2 0.5548589753846457
3 0.5548589753846458
4 0.37847201994856156
5 0.0666690046667928
/tmp/ipykernel_4748/3267321456.py:23: DeprecationWarning: `trapz` is deprecated. Use `trapezoid` instead, or one of the numerical integration functions in `scipy.integrate`.
weight = np.trapz(y=integrand, x=x)